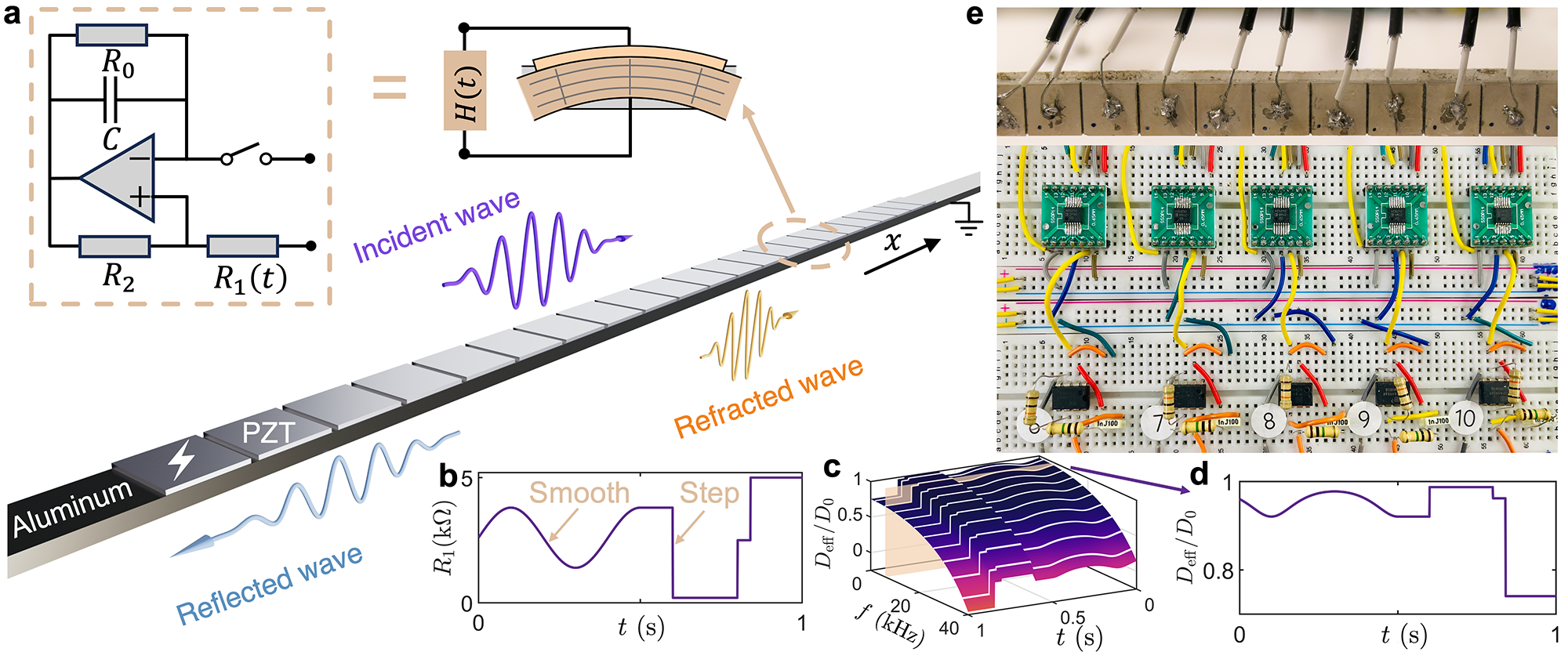
Observe Temporal Refraction and Reflection in Elastic Beams
Direct physical observation of temporal wave refraction in elastic medium has been challenging for decades due to the requirement for rapid and uniform changes in material properties. This study reports the first experimental demonstration of temporal refraction of flexure waves in a continuous mechanical system. By integrating piezoelectric patches with time-varying transfer functions, frequency conversions of flexural wave refraction and reflection are observed experimentally in a time-modulated elastic metabeam featuring single and multi-stepped temporal interfaces. These results are well interpreted using temporal Snell’s law and Fresnel’s equations for temporal interfaces. These findings could provide a new temporal framework for mechanical metamaterials, enabling unconventional wave manipulation, such as adaptive waveform shaping and advanced signal processing technologies. Learn more
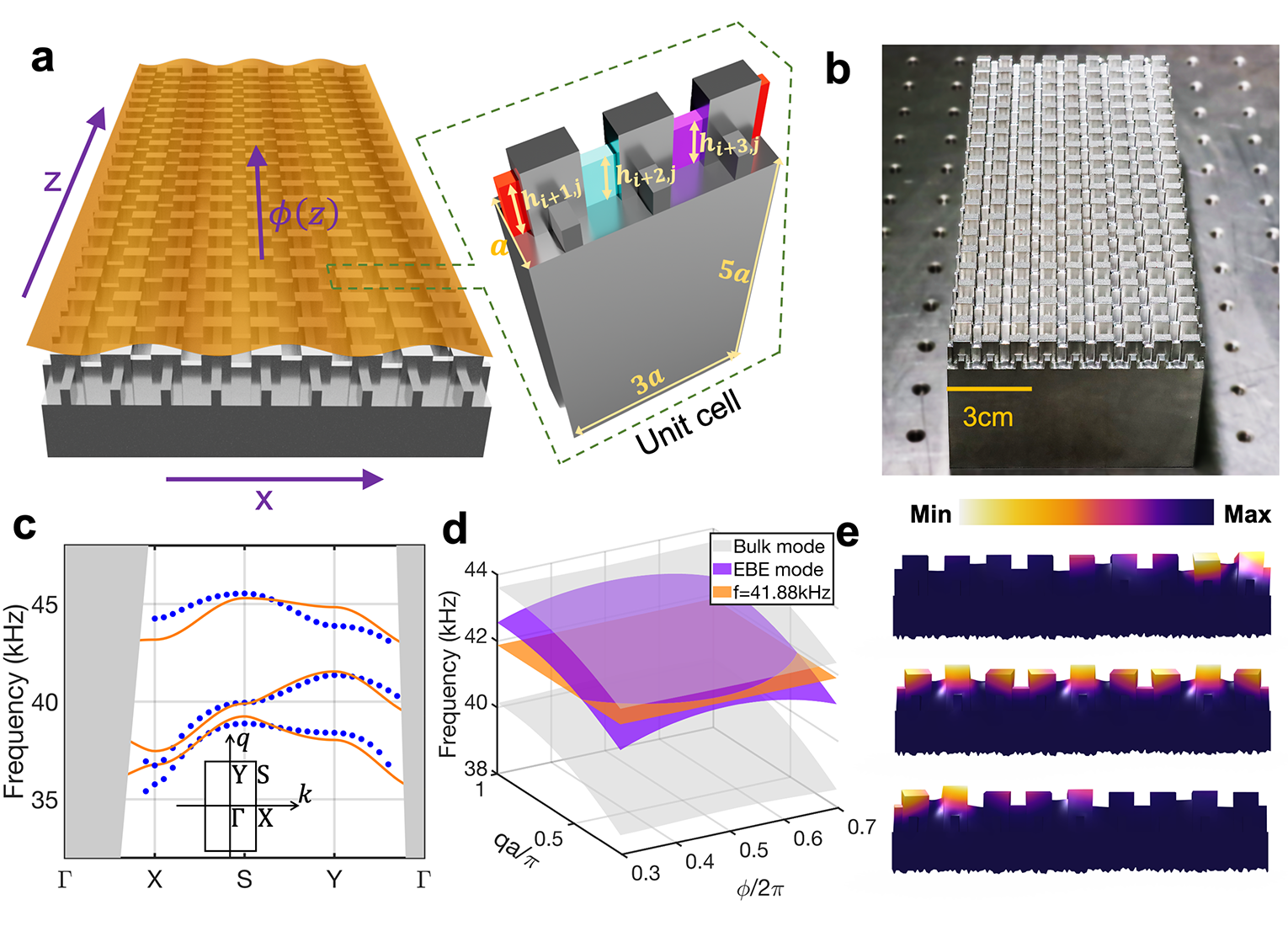
Topological Pumping of Surface Waves
Topological pumping allows waves to navigate a sample undisturbed by disorders and defects. We demonstrate this phenomenon with elastic surface waves by strategically patterning an elastic surface to create a synthetic dimension. The surface is decorated with arrays of resonating pillars that are connected by spatially slow-varying coupling bridges and support eigenmodes located below the sound cone. We establish a connection between the collective dynamics of the pillars and that of electrons in a magnetic field by developing a tight-binding model and a WKB (Wentzel-Kramers-Brillouin) analysis. This enables us to predict the topological pumping pattern, which we validate through numerical and experimental steering of waves from one edge to the other. Furthermore, we observe the immune nature of the topologically pumped surface waves to disorder and defects. The combination of surface patterning and WKB analysis provides a versatile platform for control- ling surface waves and exploring topological matter in higher dimensions. Learn more
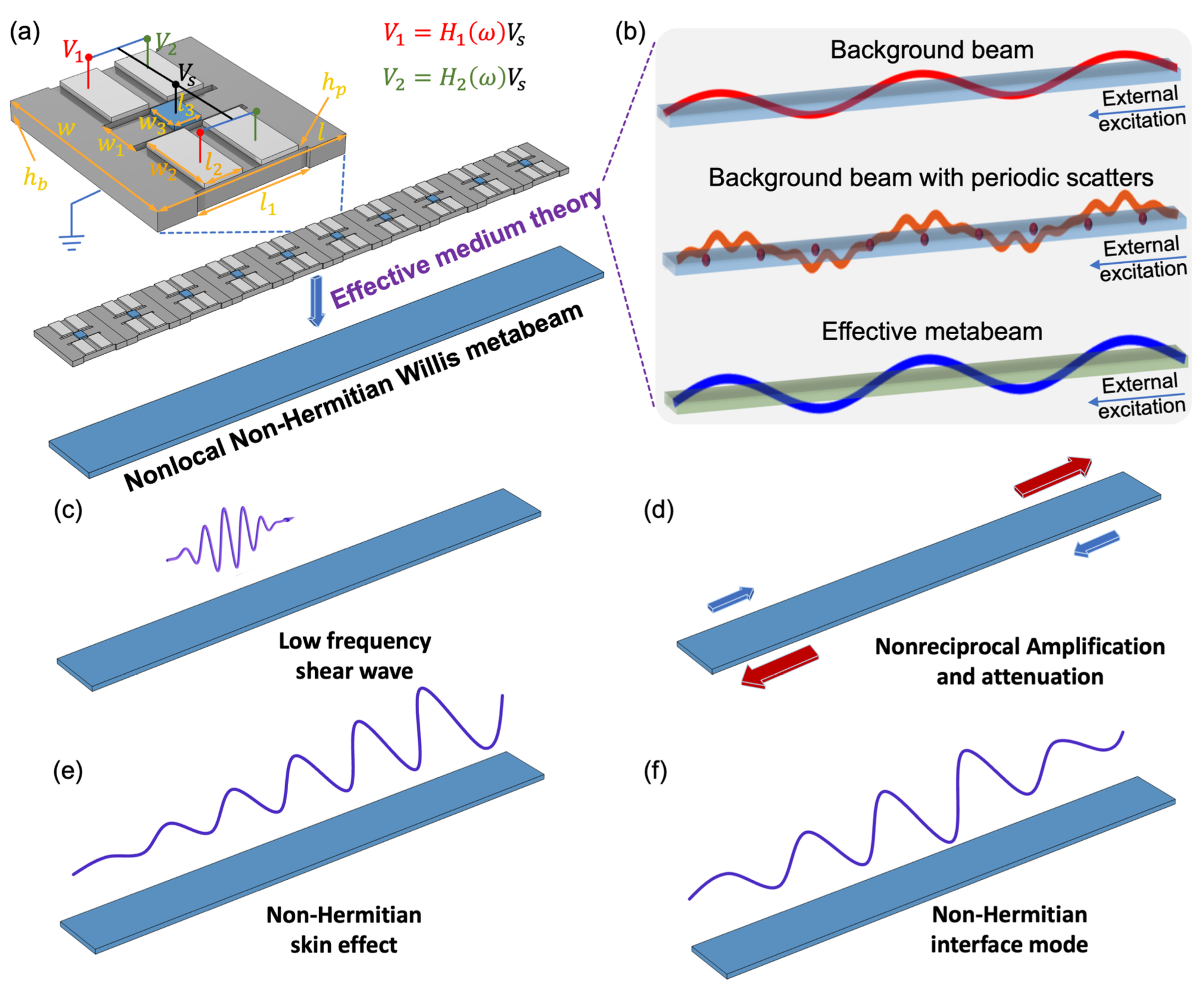
Effective Medium Theory for Nonlocal Non-Hermitian Willis Metabeams
We develop an effective medium theory (EMT) for nonlocal non-Hermitian Willis metabeams, integrating active sensor–actuator pairs to induce nonreciprocal wave behavior. Unlike classical elasticity, Willis media enable stress–velocity and momentum–strain coupling, capturing richer wave interactions. Our EMT extends beyond long-wavelength limits, accurately predicting low-frequency shear waves, direction-dependent amplification, and skin modes under open boundaries via generalized Brillouin zone (GBZ) analysis. By establishing a bulk–boundary correspondence (BBC) that links the winding number to wave localization, we provide a practical alternative to direct GBZ computation. This work advances nonreciprocal wave control, energy harvesting, and active metamaterial design with tailored functionalities. Learn more
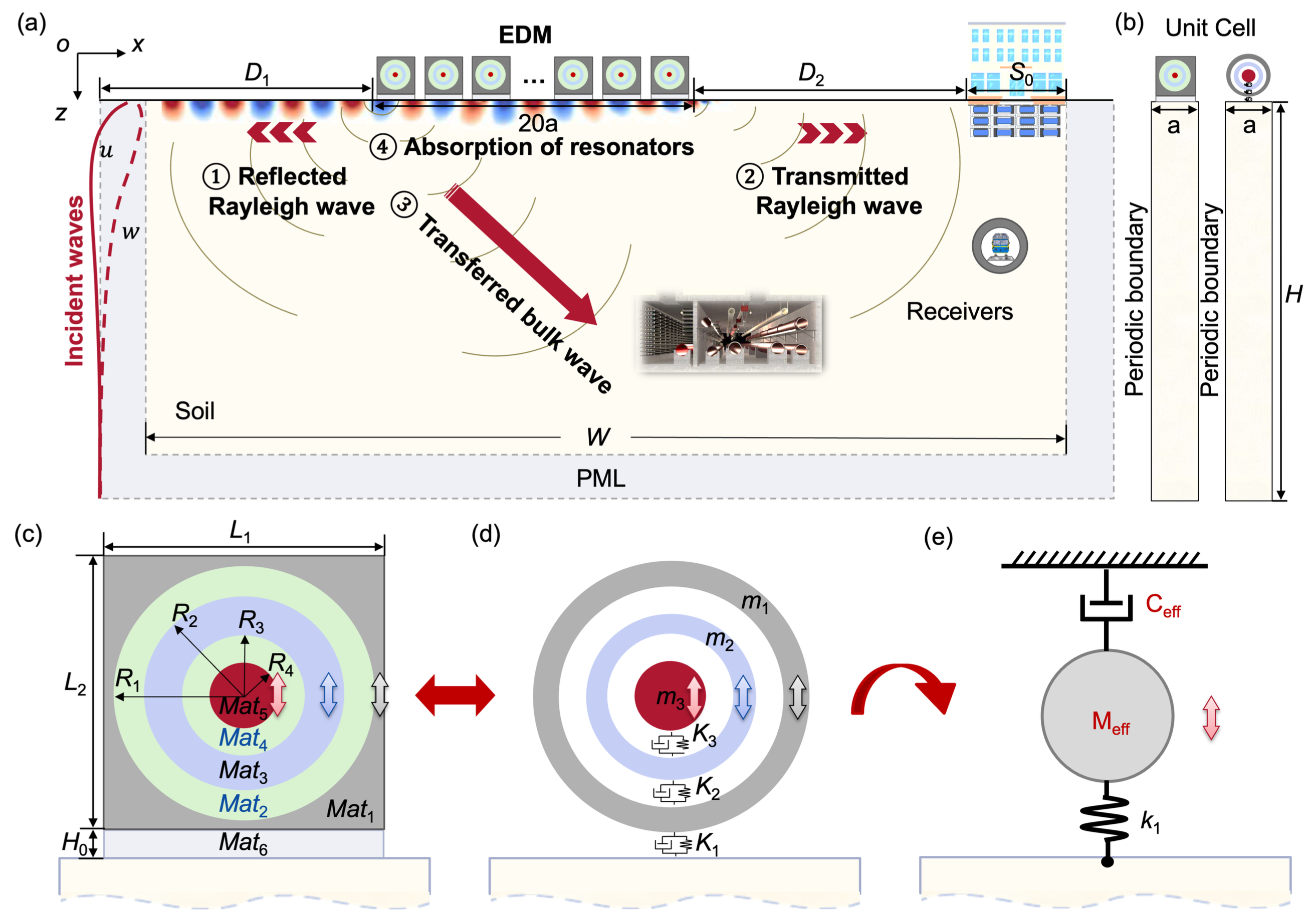
Dissipative Locally Resonant Metasurfaces for Low-Frequency Rayleigh Wave Mitigation
Low-frequency Rayleigh waves from earthquakes, traffic, and heavy machinery pose risks to structures, yet mitigating subwavelength waves remains challenging. We propose an elastic dissipative metasurface (EDM) for broadband Rayleigh wave suppression, overcoming the narrowband limitations of traditional local resonators. By integrating multi-resonant elements and damping mechanisms, EDMs create a continuous broad bandgap, effectively reducing wave transmission. Using a mass-in-mass lattice model, we reveal suppression mechanisms through negative effective mass density and metadamping effects. Additionally, a graded EDM leveraging the adiabatic theorem achieves zero reflection, perfect rainbow absorption, and efficient wave modulation. This work paves the way for next-generation metasurfaces for earthquake wave mitigation. Learn more
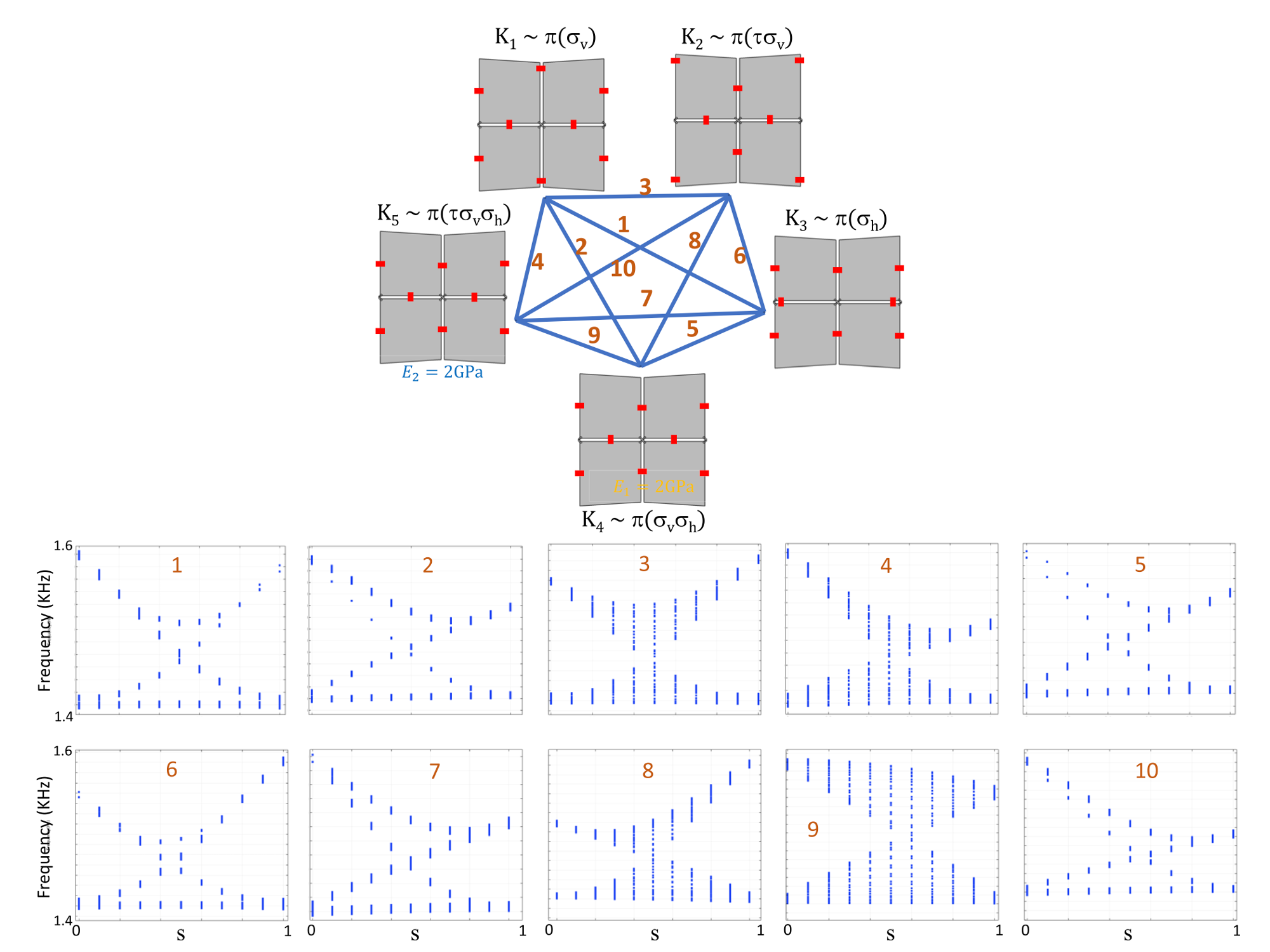
Topological Spectral Bands with Frieze Groups
This paper explores how architected materials can be designed using frieze group symmetries to generate specific topological spectral bands. The study uses tools from operator algebra and K-theory to analyze the spectral properties of these materials. It demonstrates how different topological charges are assigned to spectral bands, providing practical methods for spectral engineering. The research offers insights into constructing metamaterials with stable topological dynamics that can be adapted for experimental use. Learn more
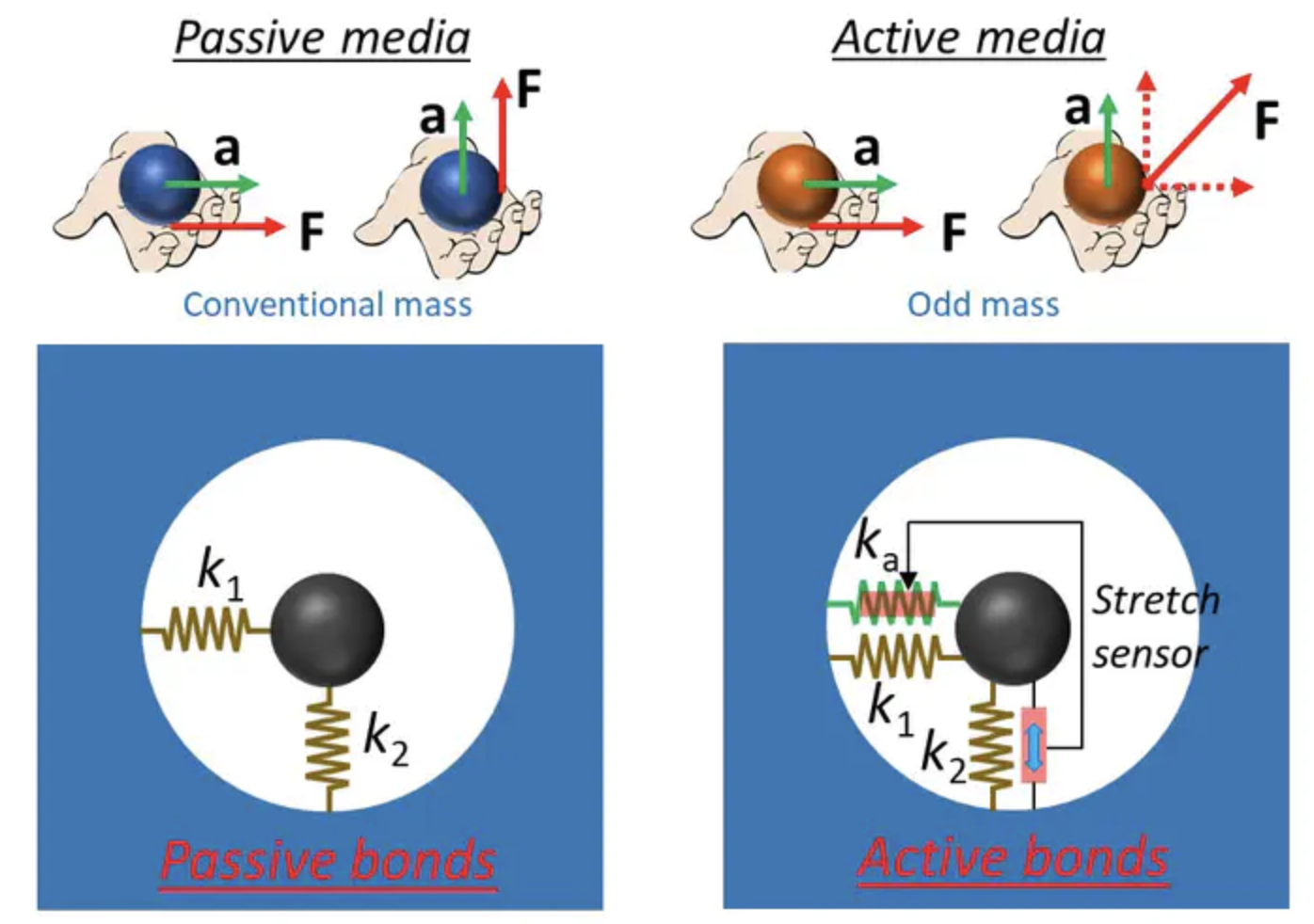
Odd Mass Density
This paper investigates active metamaterials with an odd mass density tensor, created by asymmetric active forces. These forces enable non-Hermitian wave behaviors, including directional amplification and non-reciprocal propagation, where waves travel in one direction only. The study also explores the non-Hermitian skin effect, showing wave localization at boundaries, offering insights for wave control in applications like vibration management and structural health monitoring. Learn more
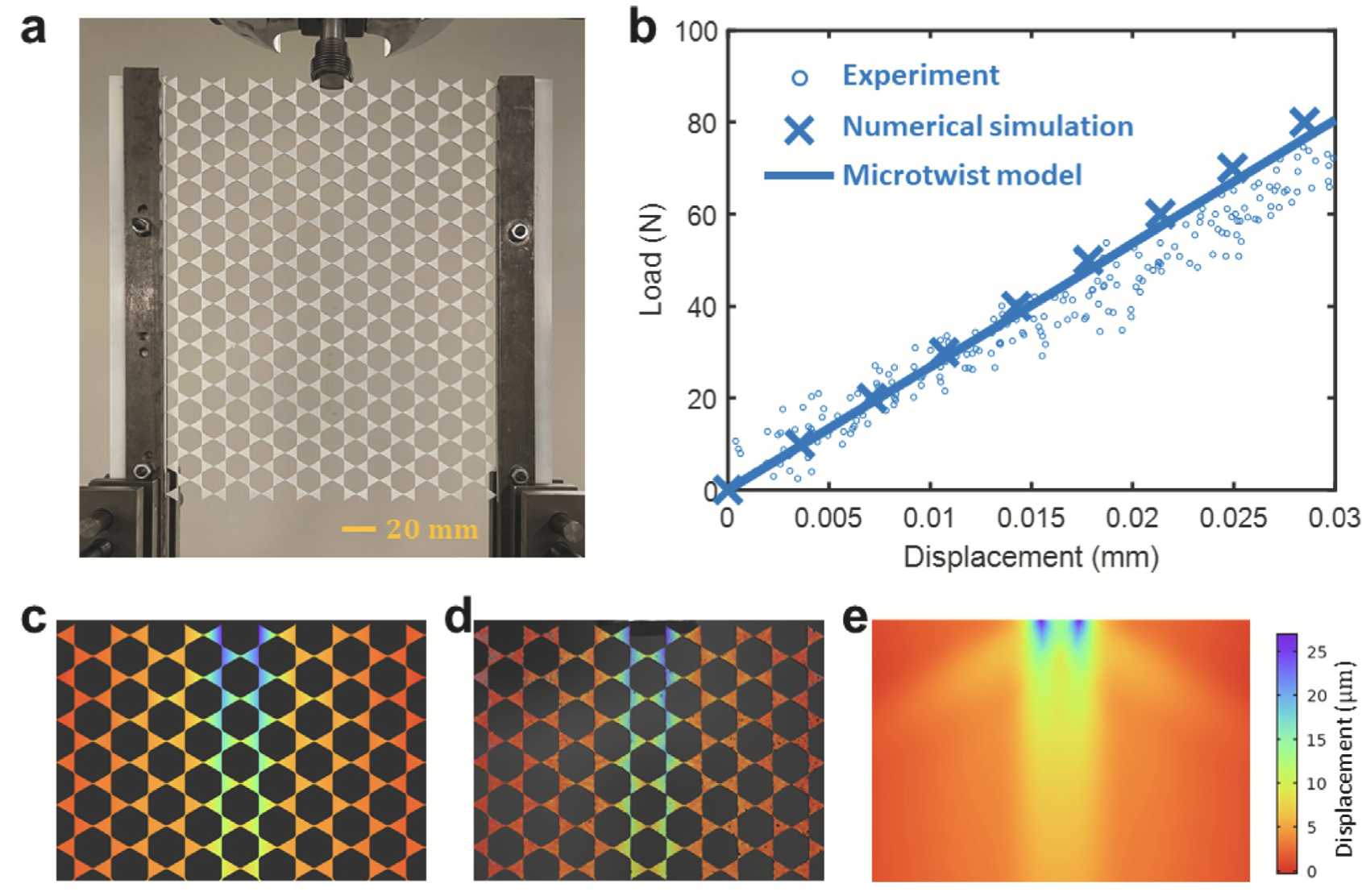
Homogenization of Twisted Kagome
This paper develops a microtwist theory to model the topological polarization and zero modes in hinged Kagome lattices. It extends traditional models by accounting for bending, shear, and stretching deformations in the ligaments that connect rigid triangles. Through both theoretical analysis and experimental validation, the study demonstrates how these lattices exhibit non-uniform deformation and asymmetric wave behaviors. The findings offer insights into designing metamaterials with programmable mechanical properties. Learn more
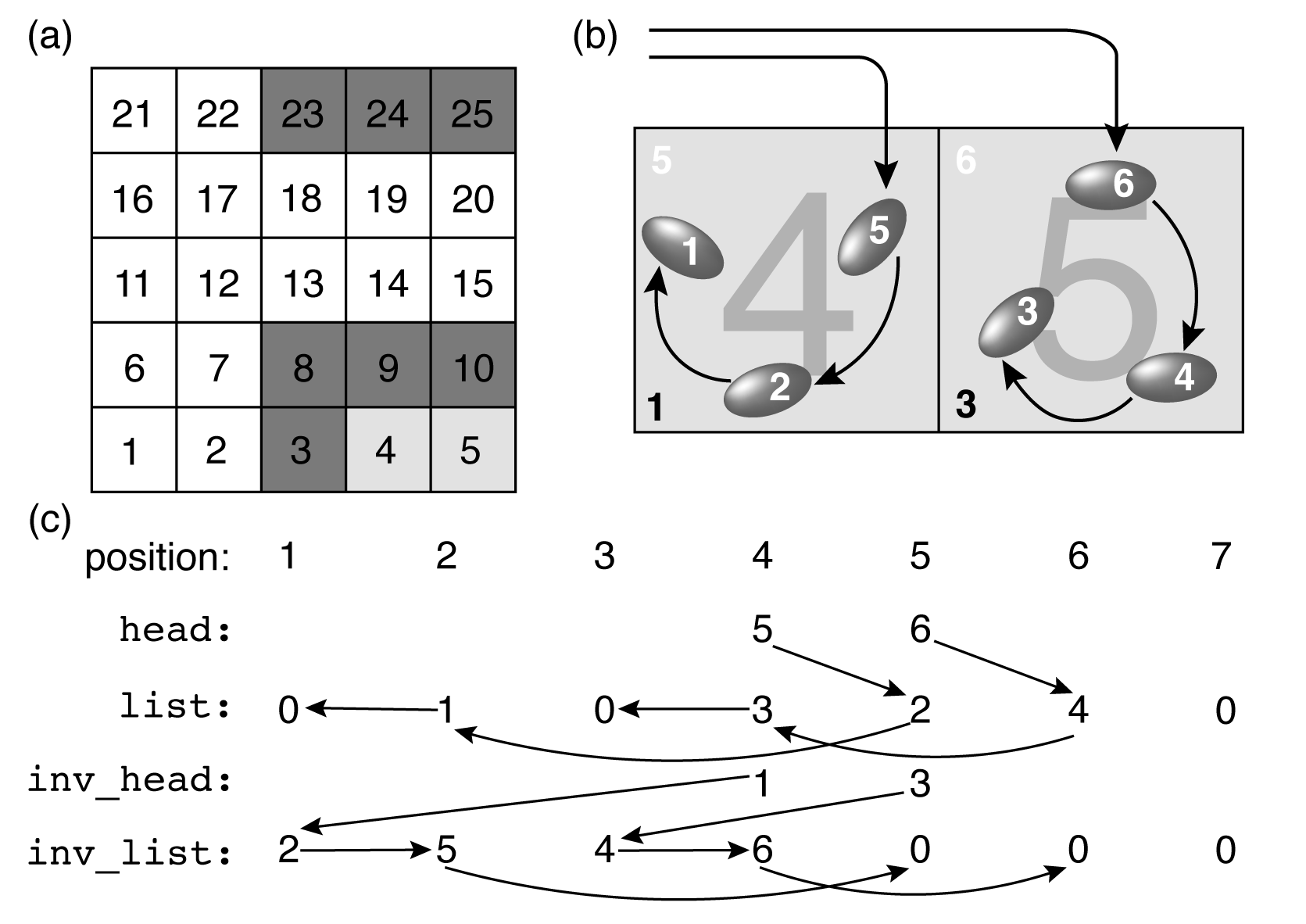
Cell List Algorithms for Monte Carlo Simulation
This paper introduces a cell lists method using doubly linked lists for efficient Monte Carlo simulations. It improves particle insertion, deletion, and nonlocal moves (e.g., pivot, reptation) where Verlet lists struggle. With O(N) complexity, the method efficiently handles large displacements in polymer simulations and Metropolis algorithms. Validated through Lennard-Jones fluid simulations, it offers better memory efficiency and scalability than traditional methods. Learn more
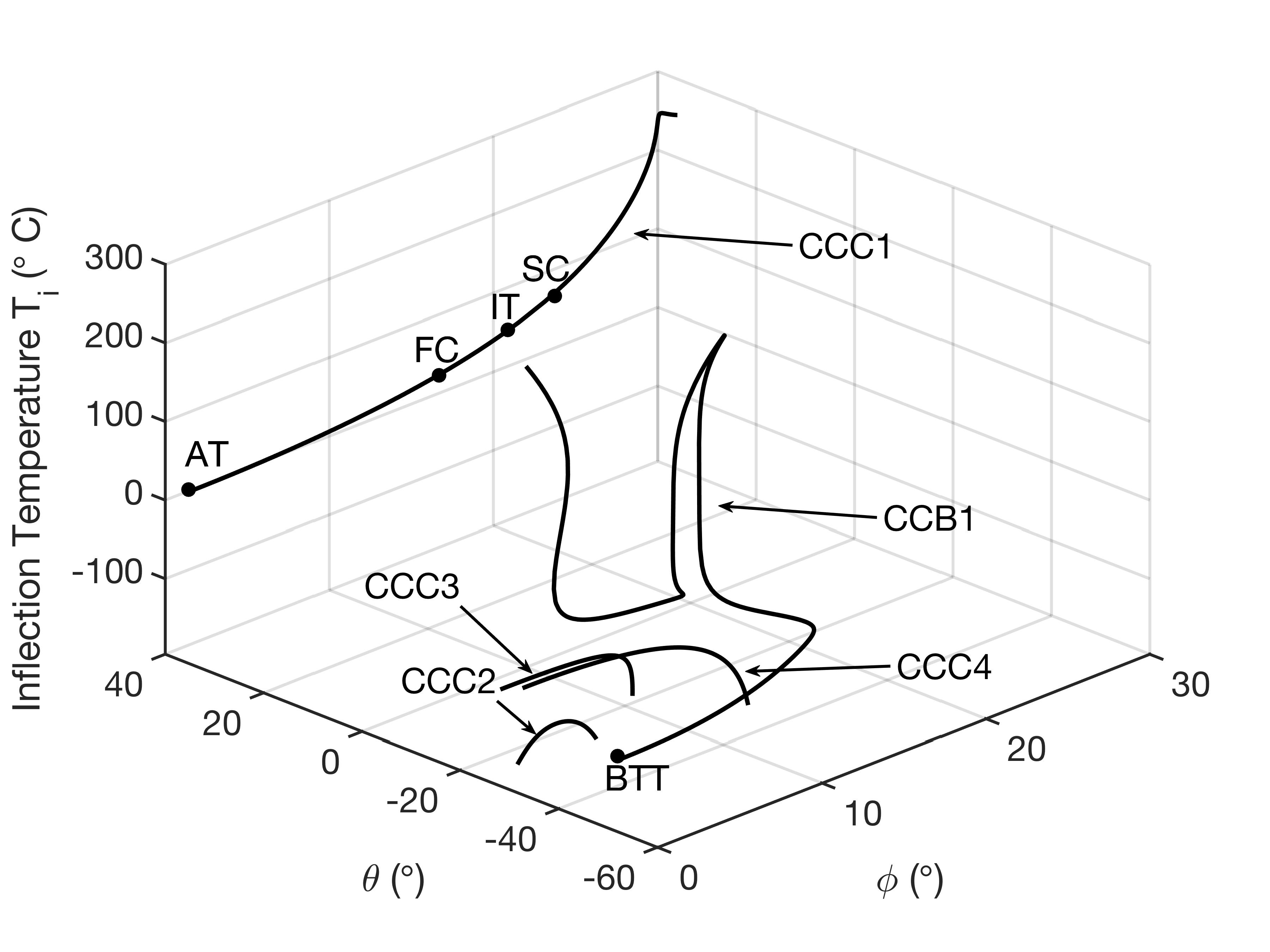
Finding Temperature Insensitive Quartz Resonator Cuts
This paper investigates the optimal orientations of quartz crystal plates with frequency-temperature relations following cubic curves. It develops a theoretical approach to solve the first and second derivatives of these relations, identifying multiple quartz cuts—including AT, FC, IT, and SC cuts—suitable for resonators in varying temperature environments. The research enhances the understanding of frequency stability, providing new insights for applications in high-precision frequency control under both high and low temperatures. Learn more
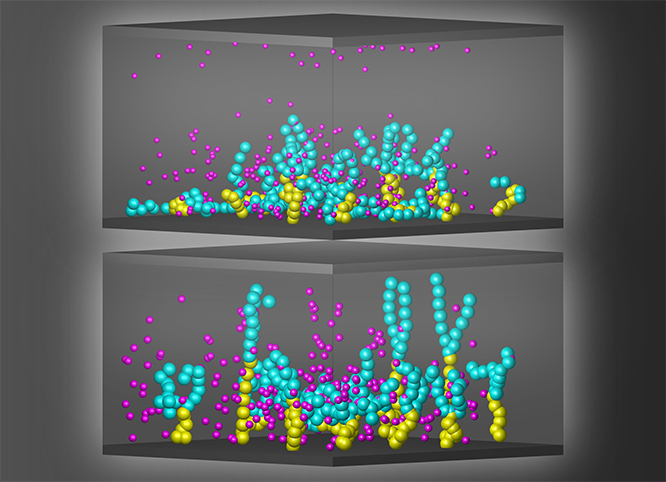
Molecular Simulation of Charged Brushes
This paper investigates the behavior of branched polyelectrolyte star brushes under external electric fields using Langevin dynamics simulations. It focuses on how polymer conformation, electrostatic interactions, and stratification are influenced by the interplay between the electric field and charged polymer chains. The study provides insights into polymer structure, screening effects, and dynamic responses, offering valuable contributions to the understanding of soft matter systems and applications involving electro-responsive materials.Learn more